For an overview of what SHACL and OWL are, and how they differ, we refer the reader to https://www.netidee.at/combining-shacl-and-ontologies/shacl-and-owl. More information om models for OWL can be found on https://www.netidee.at/combining-shacl-and-ontologies/short-introduction-models.

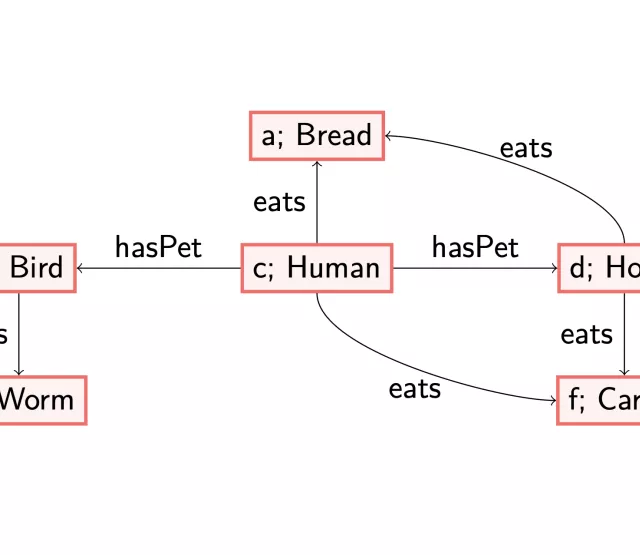
Before we get to definitions, we note that SHACL validates data graphs (or RDF structures). These can be viewed as a graph with labels on both the edges and the nodes, where multiple labels may be used at the same place. Moreover, a SHACL shapes graph is a pair containing a set of constraints and a set of targets: indications of which nodes in the data graph should validate which constraints.

This brings us to the definition: a SHACL shapes graph is satisfiable if and only if it is possible to construct a data graph such that each targeted node validates its assigned constraints.

The first question that may come to mind: why even consider satisfiability, or a decision procedure that decides satisfiability? First of all, it helps by giving insight into the complexity of different SHACL fragments. Moreover, the possibility of comparing the expressivity of different features. Clearly, there is no point in testing data graphs for validation against an unsatisfiable shapes graph: there will be nothing useful in the validation report as there is not a single update of the data graph that can fix validation. Furthermore, containment of two shapes graphs may be derived: is every data graph that validates shapes graph A also validating shapes graph B? With this kind of knowledge, shapes graphs can be simplified.

Before, we mentioned providing a decision procedure. However, this is not always possible. If this cannot be done, we call a fragment of SHACL undecidable.

Undecidability exceeds the realm of SHACL satisfiability: an example of an undecidable problem is the domino tiling problem. To understand what this problem is about, assume we are given infinitely many jig saw puzzle pieces (we may have multiple copies of the same pieces). The question is whether it is possible to combine them into an infinitely large jig saw puzzle. It may be possible to find a solution to a single case, however, it is not possible to provide a procedure that is guaranteed to give a solution within a finite amount of steps. It is known for quite a long time that this is an undecidable problem, see for instance [1].

To show that we cannot decide satisfiability of each shapes graph expressible in some SHACL fragment, we reduce an undecidable problem like the domino tiling problem to SHACL. This is done by showing we can translate each specific domino tiling problem into a shapes graph that is satisfiable if and only if the given tiling can fill an infinite grid: the infinite jig saw puzzle.

An example of an unsatisfiable fragment of SHACL is a fragment containing the path equality feature. First of all, we say something like each node needs to have a right and one up edge leaving them. Using path equality, we may express that up followed by right corresponds to the diagonal, and in the same way, we say that first right and then up is also equal to the diagonal. In this way, we already build the infinite grid that is characteristic to a jig saw puzzle. What is left to do is express the shape of the puzzle pieces: that is, rules like, if you are a puzzle piece of type A, your right neighbour has to be of types B1, B2 or B3. And: when you are a puzzle piece of type B, you are not at the same time a puzzle piece of any other type. Finally, we state that one of the nodes satisfies at least one of the types available.

The above is not the sole example of an undecidable fragment of SHACL. But luckily, there are also many decidable fragments of SHACL for which there exists a decision procedure, see for instance [2]. However, as seen here, already quite simple fragments of SHACL are undecidable and it is worth finding out which ones they are.

References

[1] R. Berger, The Undecidability of the Domino Problem, American Mathematical Soc., 1966.

[2] P. Pareti, G. Konstantinidis, and F. Mogavero, Satisfiability and Containment of Recursive SHACL, Journal of Web Semantics, 2022.