Was ist Spieltheorie?

In der Spieltheorie modelliert und analysiert man Interaktionen von zwei oder mehreren Parteien. Bei dieser Interaktion kann es sich tatsächlich um ein (Computer-, Brett-, Gesellschafts-) Spiel handeln, muss es aber nicht. Auch Kriege, Politik oder strategische Entscheidungen einer Firma können spieltheoretisch beschrieben werden. In meiner Forschung modelliere ich die Interaktionen von Blockchain Usern als Spiele und analysiere anschließend ob die Verhaltensregeln, die ein gewisses Ziel wie zum Beispiel eine "Überweisung" herbeiführen sollen, sicher  sind. Wann solche Regeln sicher  sind, wird im Laufe dieses Blogeintrags erklärt.

Arten von Spielen

Ein Spiel besteht im Wesentlichen aus drei Komponenten. Den Spielern, den möglichen Aktionen und den daraus folgenden Ergebnissen. Wie in einem Gesellschaftsspiel auch können die Spieler, wann immer sie an der Reihe sind, eine Aktion aus einer gewissen Menge von Optionen wählen. Sobald das Spiel zu Ende ist, wird jeder Spieler*in ein Ergebnis zugewiesen, zum Beispiel eine Punkteanzahl.

Das Spiel Schere-Stein-Papier hat zwei Spieler*innen, beide haben je einen Zug. Dabei können sie zwischen Schere, Stein und Papier wählen. Die Spieler*innen entscheiden gleichzeitig. Dann ist das Spiel zu Ende. Je nach Konstellation der Aktionen, gewinnt man, verliert man oder spielt unentschieden. Mathematisch wird das Spiel als Tabelle dargestellt. Spielerin 1 repräsentiert die Reihen (in blau) und Spieler 2 die Spalten (in türkis). Der Wert 0 steht für unentschieden, 1 für Sieg und -1 für Niederlage.

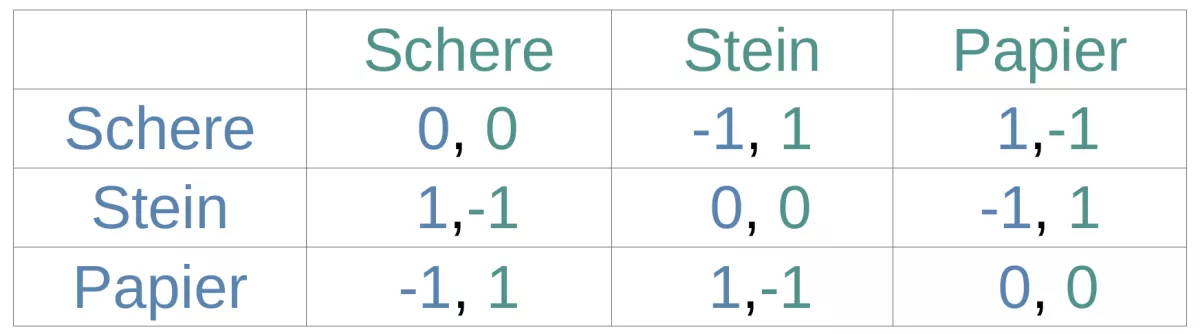
Schere-Stein-Papier ist ein Beispiel für ein simultanes Spiel, weil die Züge der Spieler*innen gleichzeitig passieren. Im Gegensatz dazu gibt es auch sequentielle Spiele, so wie Tic-Tac-Toe, wo die Züge hintereinander erfolgen. Tic-Tac-Toe ist darüberhinaus ein Spiel mit perfekter Information, das heißt alle Spieler*innen kennen alle Fakten. Spiele mit imperfekter Information sind zum Beispiel viele Kartenspiele bei denen man nur die eigenen Karten kennt (Poker, Schnapsen). Eine weitere wichtige Art von Spielen sind stochastische Spiele, das sind jene bei denen der Zufall, zusätzlich zu den Aktionen der Spieler*innen, auch eine Rolle spielt. Beispiele dafür sind Roulette und Würfelspiele im Allgemeinen.

Analyse von Spielen

Soweit so gut. Die Frage, die man sich nun als Spieler*in stellt, ist: Was ist die beste Strategie? Die Antwort darauf ist nicht so einfach. In manchen Fällen gibt es eine Winning Strategy, also eine Strategie die garantiert die höchste Punktezahl liefert. Für Anwendungen im echten Leben und auf der Blockchain ist das allerdings nur in Ausnahmen der Fall. Eine vielversprechendere Herangehensweise sind Nash Gleichgewichte. Ein Nash Gleichgewicht ist eine gemeinsame Strategie aller Spieler*innen deren Ergebnis für alle besser ist, als wenn sie alleine auf eine andere Auswahlmöglichkeit ausweichen.

Im obigen Beispiel von Schere-Stein-Papier gibt es so ein Nash Gleichgewicht nicht, denn wenn Spielerin 1 mit der gemeinsamen Strategie zufrieden ist, das heißt durch Ausweichen auf eine andere Aktion wird ihr Ergebnis schlechter (z.B. Spielerin 1 nimmt Schere, Spieler 2 wählt Papier), dann ist Spieler 2 unzufrieden und würde gerne zu Stein wechseln. Daraufhin möchte Spielerin 1 zu Papier wechseln usw.

Wann ist ein Spielverlauf sicher?

Wie in der Einleitung erwähnt, analysiert meine Forschung die vorgegebenen Verhaltensregeln in Blockchain Interaktionen. Das Einhalten dieser vorgegebenen Verhaltensregeln nennt man ehrliches Verhalten. In einem spieltheoretischen Modell einer Blockchain Interaktion stellt dieses ehrliche Verhalten einen möglichen Spielverlauf dar. In meiner Publikation, wird das ehrliche Verhalten sicher genannt, wenn es die folgenden zwei Punkte erfüllt:

1. Spieler*innen die sich ehrlich verhalten, bekommen nie ein negatives Ergebnis (einen Wert kleiner als 0), auch wenn andere "bösartig" sind.
2. Das ehrliche Verhalten bringt das beste Ergebnis. Durch eine Abweichung einer Gruppe von Usern wird deren Ergebnis schlechter.

Diese beiden Prinzipien werden durch spieltheoretische Formeln repräsentiert. Das zweite Prinzip ist im Wesentlichen eine Erweiterung des Nash Gleichgewichts.

Falls Ihr Interesse für das Thema geweckt wurde, kann ich Ihnen die folgenden leicht verdaulichen Ressourcen empfehlen: den Hollywoodfilm "A beautiful mind" über das Leben von John Nash, dem Erfinder des Nash Gleichgewichts der für seine Leistungen in der Spieltheorie den Wirtschaftsnobelpreis erhalten hat; darüberhinaus die Youtube Playlist Game Theory 101 (Englisch) und das Buch des österreichischen Mathematikers Rudolf Taschner Die Mathematik des Daseins (Deutsch).